Advanced Journal of Chemistry, Section B: Natural Products and Medical Chemistry

Current Issue

By Issue

By Author

By Subject

Author Index

Keyword Index

About Journal

Aims and Scope

Publication Ethics

Publication Cycle-Process Flowchart

Article Processing Charges

Publisher Business Model

Open Access Policy

Self-Archiving Policy

Journal’s Policies for Plagiarism, Fees and Publication

Authors Benefits

Related Links

FAQ

News

Reviewers

Peer Review Process

Peer Review Policy

Editors

Editorial Policies

Guidelines for Guest Editors

Computational Investigation for Tetragonal Crystals of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 Photocatalysts for Wastewater Treatment: First Principle Approaches

Document Type : Original Research Article

Authors

1 Department of Civil Engineering, European University of Bangladesh (EUB) 2/4, Gabtoli, Mirpur, Dhaka-1216, Bangladesh

2 Department of Civil Engineering, Michigan State University, East Lansing, Michigan, USA

3 Department of Electrical and Electronic Engineering, European University of Bangladesh (EUB) 2/4, Gabtoli, Mirpur, Dhaka-1216, Bangladesh

4 Department of Chemistry, International University of Business Agriculture and Technology, Uttara Model Town, Dhaka 1230, Bangladesh

5 Laboratory of Computational Research for Drug Design and Material Science, Department of Chemistry, College of Arts and Sciences, IUBAT—International University of Business Agriculture and Technology, Uttara Model Town, Dhaka 1230, Bangladesh

Abstract

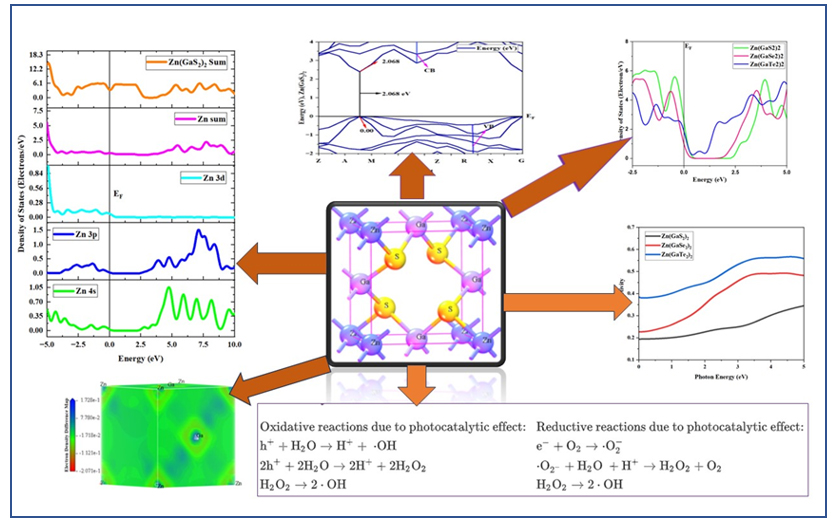
In pursuit of advancing the field of photocatalysis, a comprehensive investigation was undertaken to elucidate the electronic structure, structural geometry, and optical characteristics of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2, followed by a comparative analysis of these properties. Initial explorations involved the employment of four distinct Density Functional Theory (DFT) functionals, specifically the Generalized Gradient Approximation (GGA) with Perdew-Burke-Ernzerhof (PBE), GGA with Revised Perdew-Burke-Ernzerhof (RPBE), GGA with Perdew-Wang 1991 (PW91), and GGA with Wu-Cohen (WC) functionals, to conduct a preliminary assessment of the electronic band structures and structural configurations of the crystalline materials. However, it was noted that the band gap values for Zn(GaS2)2 exhibited variations across the different DFT functionals, registering at 2.068 eV for GGA-PBE, 2.214 eV for GGA-RPBE, 2.033 eV for GGA-PW91, and 1.936 eV for GGA-WC, where the latter value of 1.936 eV closely approximated the reference value of 1.93 eV. Consequently, the GGA-WC method emerged as the most accurate and reliable functional among the evaluated options. Furthermore, the band gap values for Zn(GaSe2)2 and Zn(GaTe2)2 were determined to be 1.726 eV and 0.329 eV, respectively, utilizing the GGA-WC functional. The total electron density was meticulously examined to delineate potential electron localization sites within the crystals, particularly concerning their capacity to activate or bond with environmental pollutants, thereby serving as efficient photocatalysts. Conspicuously, Zn(GaTe2)2 has emerged as a distinguished contender, showcasing remarkable photocatalytic effectiveness in wastewater treatment, outperforming its fellow materials. This revelation harbors substantial potential for propelling advancements in the realm of photocatalysis and environmental remediation.

Graphical Abstract

Computational Investigation for Tetragonal Crystals of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 Photocatalysts for Wastewater Treatment: First Principle Approaches

Keywords

Main Subjects

Full Text

Introduction

The paramount exigency of confronting the world's imminent water challenges with sustainable and exceedingly efficacious solutions cannot be overemphasized. The abrupt surge in global population, the expeditious march of industrialization, and the burgeoning sprawl of urban agglomerations have exerted prodigious duress upon our invaluable aqueous reservoirs, accentuating the acute necessity for cutting-edge water treatment modalities. Within this overarching purview, photocatalysis emerges as a luminous beacon of optimistic anticipation. This sophisticated methodology harnesses the formidable vigor of electromagnetic radiation to engender photoexcitation in designated semiconducting substrates, thereby effectuating catalytic metamorphoses in target molecular species. Photocatalytic technology is widely recognized as a powerful tool for wastewater treatment, with applications spanning various sectors, including textiles, ready-made garments, pharmaceuticals, paints, and residential settings [1,2]. The escalating volume of waste generated by these industries presents a substantial challenge, posing significant risks to aquatic and terrestrial ecosystems while contributing to overarching issues such as global warming and environmental degradation [1, 2]. For instance, let us consider the textile industry, which independently consumes a staggering 1.8 billion cubic meters of water annually, leading to groundwater depletion and potential health hazards for local communities [1]. Moreover, the industrial and domestic sewage discharged from these sectors collectively amounts to approximately 13,468 minimum liquid discharge (MLD) units of wastewater, of which only 60% undergoes proper treatment to remove hazardous chemicals [3]. Consequently, there is a dwindling supply of freshwater resources, with particularly severe consequences in regions like Bangladesh, where the textile industry relies heavily on water consumption [3]. The wastewater from these industries contains a hazardous mixture of organic dyes, pigments, polymers, and fabric residues, posing substantial threats to aquatic and terrestrial organisms [1]. Furthermore, the excessive use of water across residential, industrial, and agricultural sectors compounds the decline in groundwater levels, exacerbating the ongoing crisis [1]. In addressing these formidable challenges, the necessity of water recycling and reuse has risen to prominence as a compelling alternative to ensure environmental sustainability. Among various methods at our disposal, photocatalysts and photocatalysis have gained significant traction due to their multifaceted impacts and inherent advantages. Remarkably, photocatalysis has assumed a prominent role in environmental research, owing to its sustainable characteristics and capacity to offer substantial contributions to energy transformation and ecological conservation [4, 5]. What distinguishes photocatalysis as a technology of remarkable import lies in its proficiency in decomposing organic contaminants through the generation of reactive oxidation species (ROS) upon photon absorption, the energy of which aligns with or surpasses their respective band gaps. This attribute renders photocatalysis remarkably adaptable to a broad spectrum of environmental scenarios [6]. At the core of the photocatalytic process resides the photo-induced generation of electron-hole pairs, a pivotal phenomenon that subsequently engages with water and oxygen, yielding hydroxyl and superoxide radicals-a role underscored by previous research for the efficient degradation of organic pollutants [7,8]. Photocatalysts manifest as the exemplars of an environmentally conscientious and sustainable oxidation process for wastewater purification. They are characterized by their cost-effectiveness, facile manipulability, robust stability, and minimal toxicity [9-15]. These materials feature a relatively straightforward reaction system with abbreviated processing durations and exhibit the potential for reusability and recycling. Furthermore, photocatalysts do not deplete the vital resource of oxygen, evince inherent self-regeneration capabilities, and exhibit high absorptivity in the UV or sunlight spectra. Consequently, photocatalytic technology has progressively become more accessible and alluring to researchers in the field [1]. Nevertheless, it is imperative to acknowledge that current photocatalytic technology continues to grapple with limitations that impede its full-scale industrial deployment. Among the most formidable challenges is developing an ideal photocatalyst endowed with four cardinal attributes: heightened photocatalytic efficiency, an expansive specific surface area, optimal harnessing of solar irradiance, and recyclability [16-18]. Photocatalysts derived from semiconductors, including SnO2, WO3, TiO2, CeO2, and ZnO, have demonstrated remarkable UV light absorption and performance [19,20]. However, the ongoing pursuit of alternative materials potentially enhancing these characteristics persists. Notably, titanium dioxide (TiO2) and zinc oxide (ZnO) find extensive use in the photocatalytic degradation of organic pollutants owing to their superior oxidation potential, photostability, and non-toxic nature [21]. Nevertheless, their limited applicability to visible light and low quantum yields are significant drawbacks that hinder their effectiveness as photocatalysts. Extensive research has shown that enhancing the photocatalytic activity of these materials can be achieved through shape modification, such as doping with transition metals [10,16,22-23] and non-metals [23-26], or by formulating compound photocatalysts using various semiconductors [27,28]. These modifications result in a broader light absorption spectrum, simultaneously leading to increased efficiency in the dissociation of electron-hole pairs [29]. Consequently, the paramount objective of this study is to provide innovative theoretical insights based on band gap theory, thereby pushing the boundaries of knowledge in photocatalytic materials. The judicious selection of the selenium (Se) atom as an integral constituent of the photocatalyst was predicated upon its remarkable surface area, symbolic of a catalyst poised to exhibit elevated reactivity [30-32]. In a parallel vein of scholarly inquiry, Ren et al. [33] undertook a comprehensive scrutiny of the structural, electronic, and optical attributes inherent to Zn-substituted Cu(GaS2)2, scrutinizing various substitution sites through the judicious employment of the first-principles approach. Their discernments intimated that the incorporation of zinc (Zn) could facilitate the reflectivity characteristics of Zn(GaS2)2 to a discernible extent within the 1-5 eV spectral range, thereby concurrently augmenting the absorption coefficient, particularly pertinent to solar cell applications within the lower energy spectrum. First-principles calculations have garnered precedence as the preferred modality for probing the nonlinear optical (NLO) properties of materials, with a particular emphasis on their second harmonic generation (SHG) propensities on account of their prescient predictive capabilities and systematic methodological rigor [34]. In this inquiry, we harnessed computational methodologies to orchestrate the conception of innovative metal quarter crystals, specifically denominated Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2. Subsequently, we undertook a comprehensive comparative analysis of their salient attributes, harnessing the computational prowess of four distinct Density Functional Theory (DFT) functionals, namely the Generalized Gradient Approximation (GGA) with Perdew Burke Ernzerhof (PBE), the Revised Perdew Burke Ernzerhof functional (RPBE), the Perdew-Wang-91 (PW91) functional, and the Wu-Cohen functional, thus availing ourselves of state-of-the-art computational techniques. This rigorous examination was conducted with meticulous discernment, aimed at critically evaluating the merits and demerits inherent to each functional choice. Given the conspicuous empirical correlation between an attenuated band gap and augmented photocatalytic activity, our research was steadfastly dedicated to comprehensively exploring the band gap concept. To do so, we aspired to elucidate the inherent behavioural characteristics of the resultant crystals, thereby establishing their compelling candidacy for potential deployment in photocatalytic applications, particularly within the purview of wastewater treatment, where their prowess holds the promise of significant advancement.

Experimental

Methods of working procedure

 Within the CASTEP module of Material Studio version 8.0 [35], an array of Generalized Gradient Approximation (GGA) functionals are made available, presenting a diverse suite of computational analysis methods. In the ambit of our research, we judiciously selected four discrete functionals, specifically the GGA functionals complemented by the Perdew Burke Ernzerhof (PBE) approximation, the Revised Perdew Burke Ernzerhof functional (RPBE), the Perdew-Wang-91 (PW91) functional, and the Wu-Cohen (WC) functional. In the absence of empirical validation through experimental data, we harnessed these functionals to execute a comparative, first-principles examination concerning the fundamental properties of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 crystals, a systematic approach designed to yield results of commendable accuracy. Initially, the structural geometry and electronic band structures of the crystals above were meticulously ascertained, leveraging the computational prowess of the selected quartet of GGA functionals. This endeavor encompassed an optimization process, a strategic quest to minimize the system's energy level. This optimization was conducted while considering a cutoff energy value set at 400 electron volts (eV) and a k-point mesh of dimensions 4×4×4 for Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 crystals, with the incorporation of Koelling-Hamon potentials and the judicious utilization of norm-conserving pseudopotentials. Subsequently, the structural geometry and electronic characteristics of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 were probed once more, this time employing the optimized crystal structures within the purview of the four GGA functionals, all executed under the established conditions. It is noteworthy that, among these employed functionals, the GGA functional paired with the Wu-Cohen approximation manifested as the clear standout, delivering outcomes that closely paralleled experimental data, most notably in terms of band gap magnitude. Consequently, this particular function was leveraged to perform a comprehensive array of calculations, encompassing the elucidation of Density of State (DOS), Total Density of State (TDOS), and Partial Density of State (PDOS). In addition, the assessment encompassed an in-depth examination of optical properties, including absorption energy, deformation energy, catalytic energy, and electron density mapping, thus providing a comprehensive insight into the intriguing facets of these crystalline materials.

Results and Discussion

Optimized structure of studied crystals and structural geometry

The outcomes of our simulation endeavors, which encompass the optimal structural configurations, are displayed in Fig 1. Furthermore, we have meticulously listed the relevant parameters and discernments pertaining to the three distinct crystal variants in Table 1. To facilitate an exhaustive and systematic analysis of these crystalline materials, each variant has been intentionally engineered to manifest a tetragonal structure while rigorously adhering to the space group configuration (111 P-42M). Furthermore, it is pertinent to note that the densities of these crystals exhibit distinctive values, with a density of 3.82 grams per cubic centimeter (gm/cm³) for Zn (GaS2)2, 3.97 gm/cm³ for Zn(GaSe2)2, and 8.2 gm/cm³ for Zn(GaTe2)2. This observed trend in density corresponds to the ascending order of atomic mass, where Te possesses a greater atomic mass than Se, and Se, in turn, surpasses S in atomic mass. This increment in density aligns harmoniously with the atomic mass hierarchy observed across these elements.

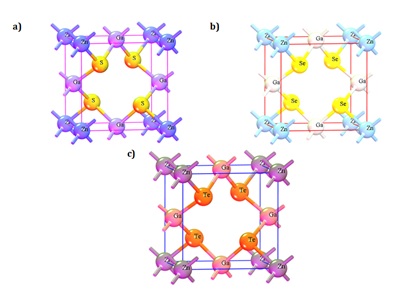
Fig 1.a) Refined configuration of Zn (GaS2)2, b) refined configuration of Zn(GaSe2)2, and c) refined configuration of Zn(GaTe2)2

Calculated band gap

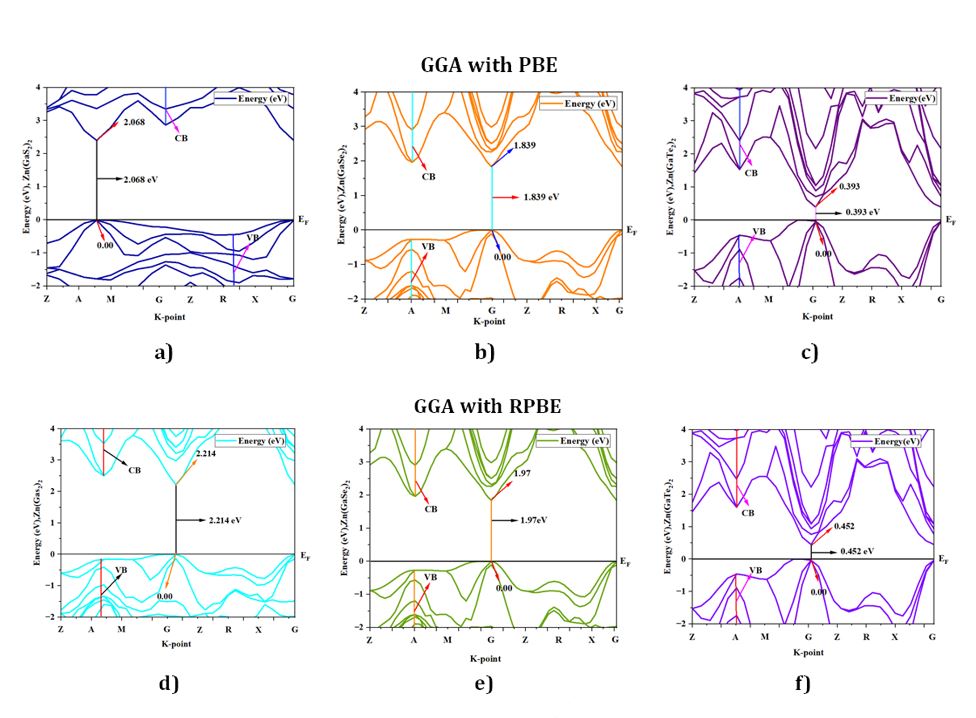
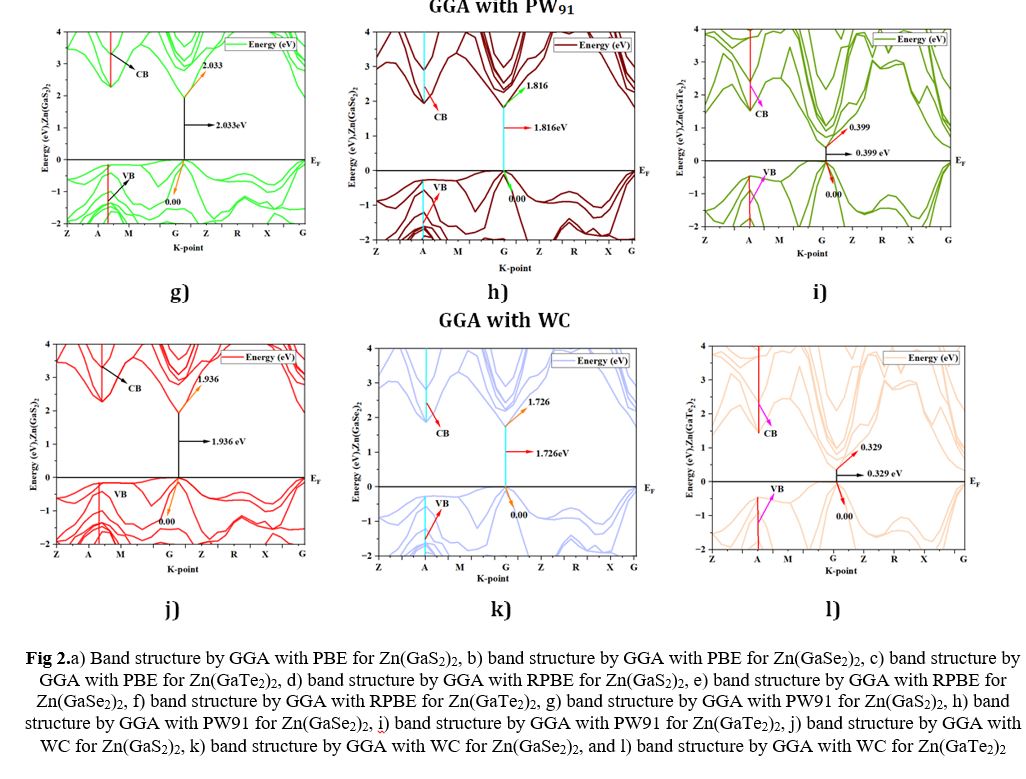
The data in Table 2 provides a comprehensive overview of the band gap values obtained for Zn (GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2, as determined through the utilization of four distinct density functional theory (DFT) methods: (GGA-PBE), (GGA-RPBE), (GGA-PW91), and (GGA-WC). The reference band gap value of 1.93 electron volts (eV) for the Zn (GaS2)2 crystal has been included in the table for reference. Our rigorous theoretical calculations yielded a band gap value of 1.936 eV, a result strikingly in accordance with the experimental data when employing the GGA-WC functional [citation]. Given this remarkable alignment, our study proceeded to delve deeper into exploring other salient material properties, with the GGA-WC practical serving as our preferred and judiciously selected computational methodology.

Electronic Structures

Semiconductor materials are characterized by their electronic band structure, which consists of a valence band (VB) with lower energy levels and a conduction band (CB) with higher energy levels. The region separating the CB from the VB is commonly called the band gap. To determine the band gap of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2, we established the Fermi energy level as the reference zero-energy point. This critical calibration was achieved by employing four distinct Density Functional Theory (DFT) functionals, accessed through CASTEP in Material Studio 8.0, as presented in Table 2. An examination of Fig 2 (a)-(l) revealed a consistent alignment of the G symmetry point with the minimum of the conduction bands (MCB) and the maximum of the valence bands (MVB) across all crystal structures, indicative of direct band gaps. The direct band gaps for Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 were calculated as 2.068 eV, 1.839 eV, and 0.393 eV, respectively, when utilizing the GGA-PBE functional. Direct band gaps imply a more efficient path for electron transitions from the VB to the CB, signifying higher photocatalytic activity. When employing GGA with RPBE, the direct band gaps for Zn (GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 were calculated as 2.214 eV, 1.97 eV, and 0.452 eV, respectively. In addition, the tetragonal forms of these crystals exhibited band gaps of 2.033 eV, 1.816 eV, and 0.399 eV, respectively, when utilizing the GGA-PW91 functional, as depicted in Figure 2. The GGA method using the WC functional was employed to determine the band gap values of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 under comparable conditions, yielding band gap values of 1.936 eV, 1.726 eV, and 0.329 eV, respectively. To conduct a comparative analysis of the four distinct methods (GGA-PBE, GGA-RPBE, GGA-PW91, and GGA-WC) on identical geometries of Zn (GaS2)2, Zn (GaSe2)2, and Zn (GaTe2)2, the computed band structures were examined. The investigation revealed that the MCB and MVB displayed similar oscillations, albeit with distinct patterns among the various GGA methods, with GGA-RPBE exhibiting the most significant deviations. Notably, the use of the GGA-WC functional resulted in a band gap value of 1.936 eV for Zn (GaSe2)2, closely aligning with the experimental value of 1.93 eV. Consequently, the GGA-WC method has been unequivocally established as the reference approach for all subsequent calculations.

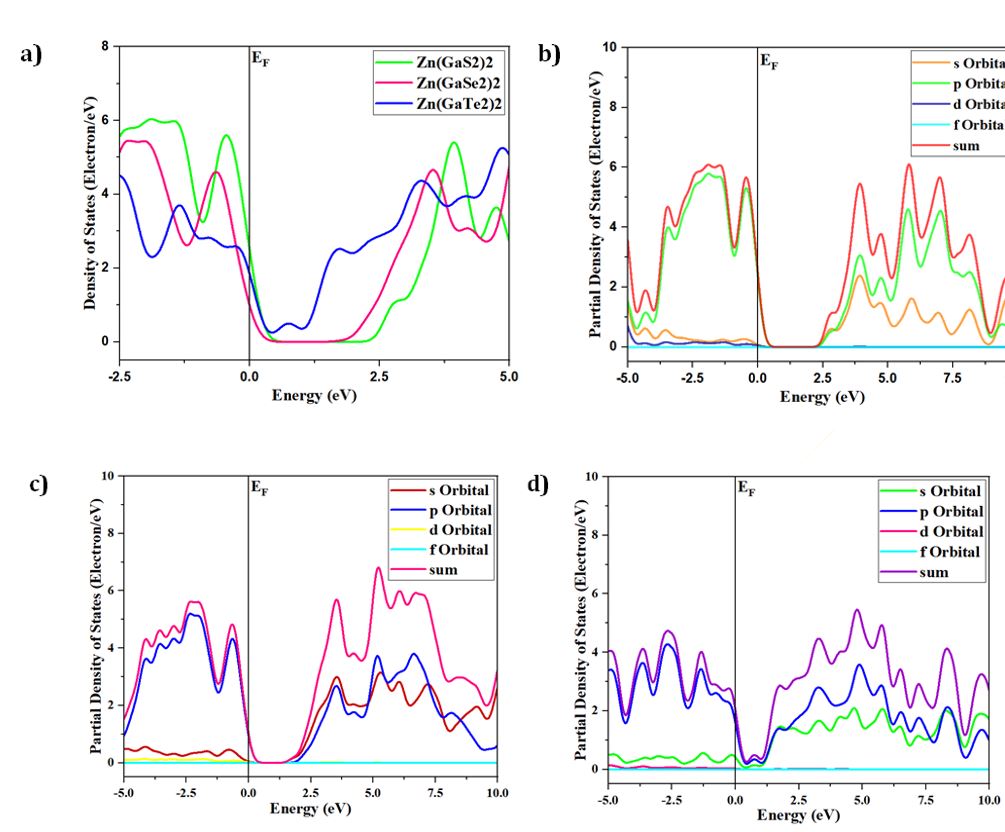
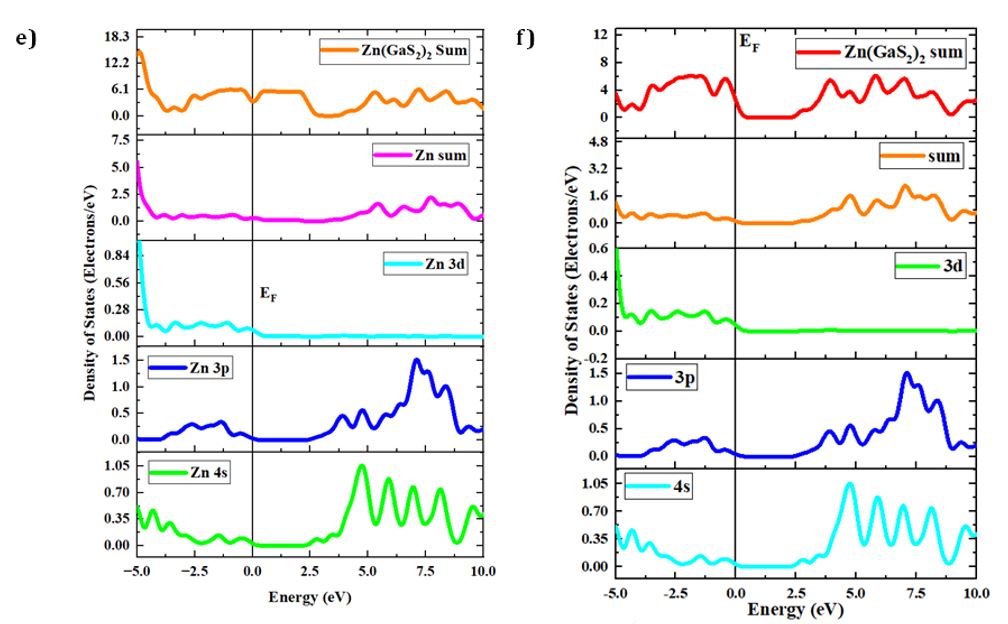
Density of States (DOS) and Partial Density of States (PDOS)

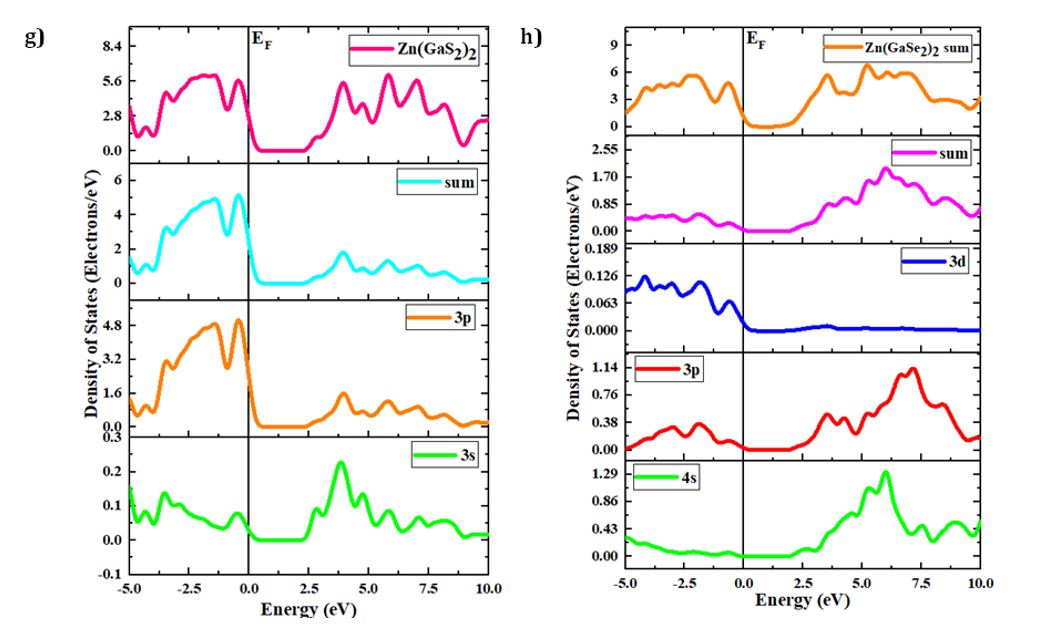
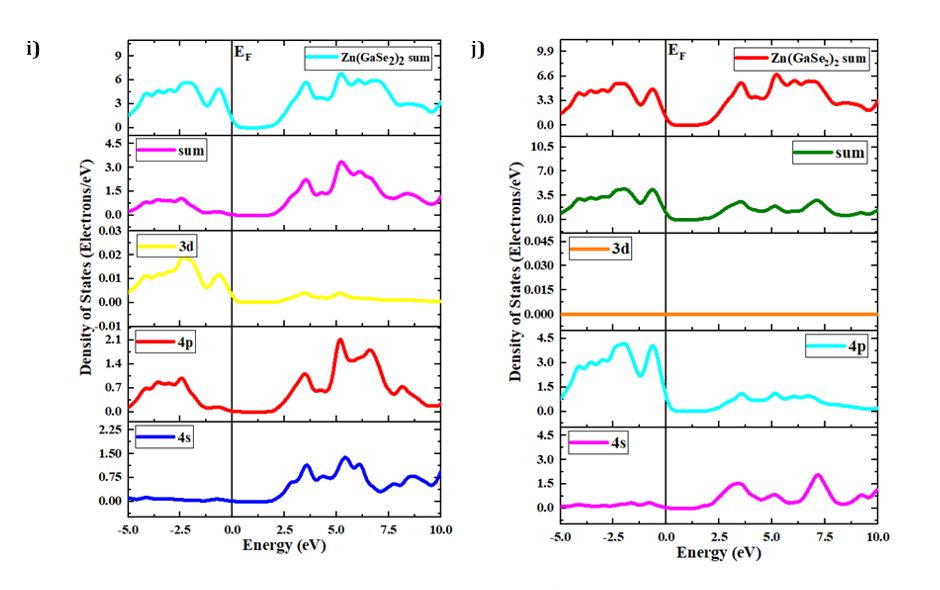
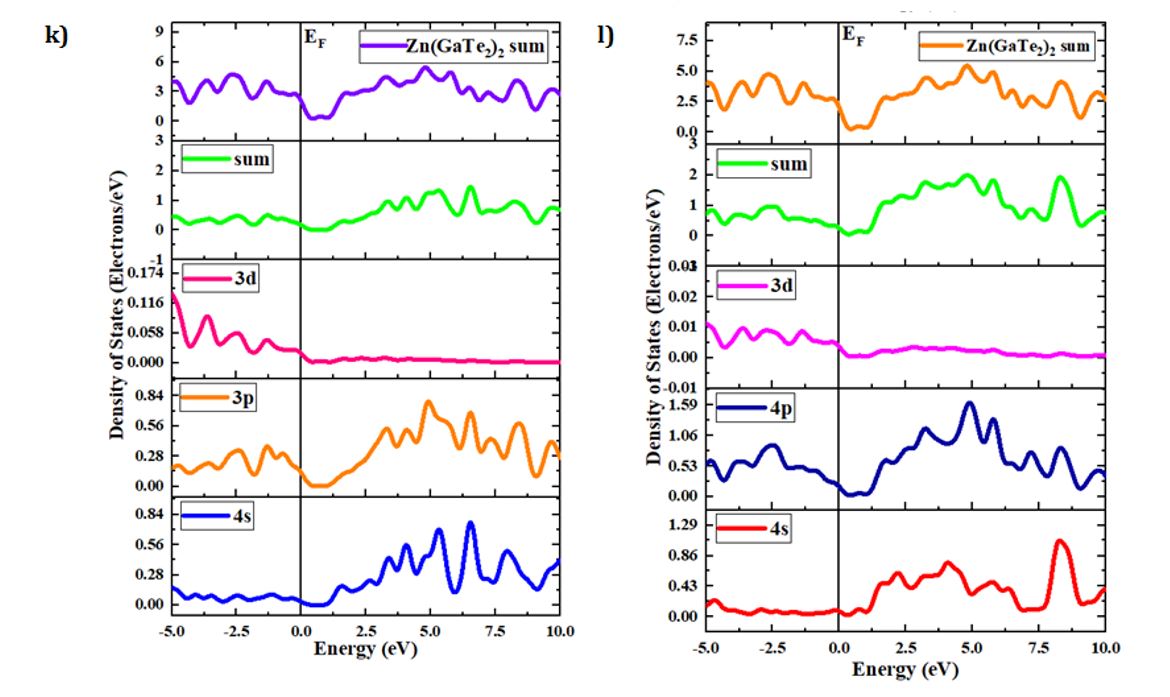
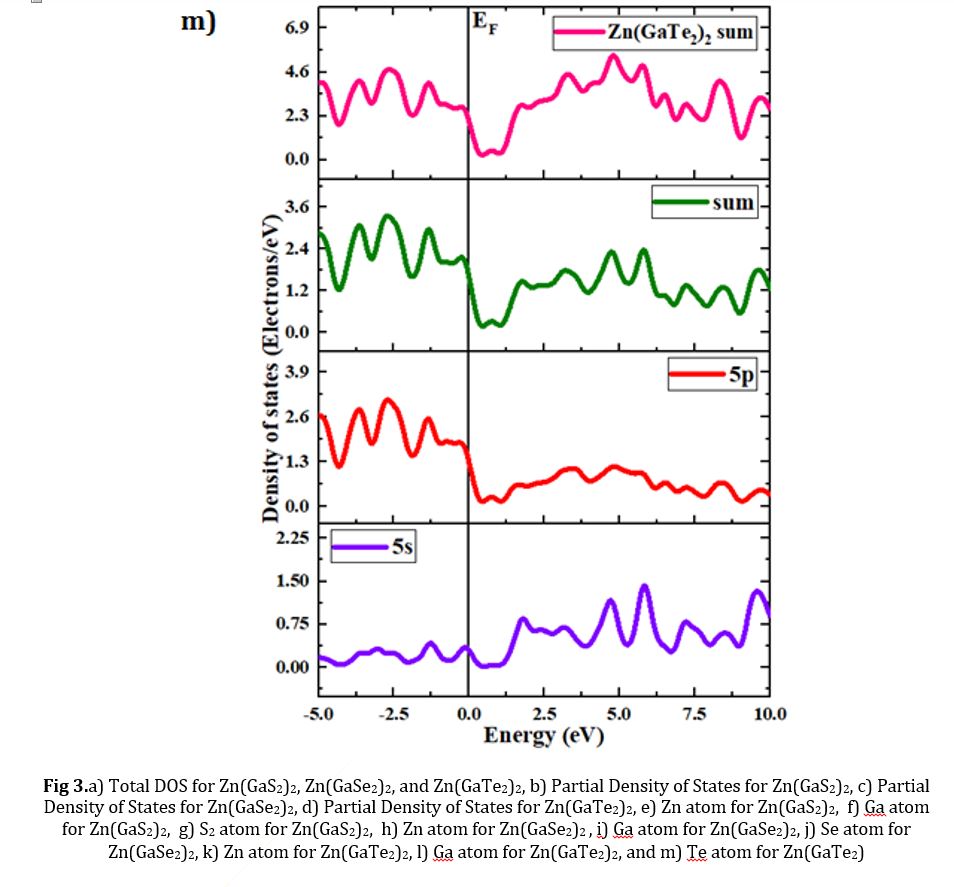
The concepts of density of states (DOS) and partial density of states (PDOS) are intricately interwoven with the electronic contributions stemming from orbital systems. These fundamental principles provide invaluable insights into the arrangement and origin of electronic band structures driven by electrons. In the present investigation, we explore the total density of states (TDOS) of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2, comprising the elements Zn, Ga, S, Se, and Te, as illustrated in Fig 3(a)-(m). The state density serves as a reliable indicator of the characteristics of electronic band structures and the allocation of orbital contributions. Notably, Density of States (DOS) and Partial Density of States (PDOS) establish direct connections with crucial chemical reactivity descriptors, encompassing the Highest Occupied Molecular Orbital (HOMO), Lowest Unoccupied Molecular Orbital (LUMO), and the HOMO-LUMO gap. These descriptors play pivotal roles in the computation of essential properties such as ionization potential, electronegativity, hardness, softness, and electron affinity for crystals. Please refer to the provided references for comprehensive insights into these calculations [36, 37]. The Highest Occupied Molecular Orbital (HOMO) coincides with the valence band, while the Lowest Unoccupied Molecular Orbital (LUMO) corresponds to the conduction band. Within the context of the photocatalytic mechanism, organic pollutants undergo degradation through reactions with ⋅O-2 and ⋅OH free radicals. The extent of degradation hinges upon the generation of ⋅O-2 and ⋅OH radicals, making the introduction of catalysts into H2O a pivotal factor in the production of ⋅O-2 and ⋅OH for photocatalysis. In this investigation, the Generalized Gradient Approximation (GGA) method, specifically employing the Perdew-Burke-Ernzerhof (PBE) functional, was utilized to compute the density of states (DOS) and partial density of states (PDOS) for the constituent elements, namely Zn, Ga, S, Se, and Te, within the crystalline structures of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2. Numerous references are available for the computation of DOS and PDOS using the GGA technique [38, 39], and in this study, the aforementioned functional method was explicitly adopted. The findings presented in Fig 3(a) indicate that the relative contributions of the orbitals of Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 account for the properties of the valence band (VB) and conduction band (CB), as evidenced by the density of states (DOS) and partial density of states (PDOS) analyses. These results suggest that the crystals exhibit p-type conductivity characteristics. Notably, within the energy range of 0-2 electron volts (eV), Zn(GaS2)2 demonstrates significantly higher values in both the valence band (VB) and conduction band (CB) when compared to Zn(GaSe2)2 and Zn(GaTe2)2. Zn (GaTe2)2 has the highest TDOS value among these crystals. An examination of Fig 3(b), (c), and (d) reveals that the p orbital exerts a substantial influence on both the CB and VB in all three compounds, namely Zn (GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2. In Fig 3(e)-(m), it is evident how individual atoms contribute to the generation of the Density of States (DOS) and Partial Density of States (PDOS). These figures illustrate that the individual atoms within each crystal actively contribute to the Partial Density of States (PDOS) by displaying favorable values in the Conduction Band (CB). This cumulative contribution of constituent elements to the Total Density of States (DOS) ultimately manifests n-type conductivity.

 

 

Optical properties

Photocatalysts rely on a myriad of active sites, encompassing various factors such as light absorption, charge mobility, band gap, and the efficient transport of electron-hole pairs. All these factors profoundly influence the conductivity, reflectivity, refractive index, and loss function of these materials. Furthermore, the substantial surface area of the material assumes a pivotal role in the adsorption of contaminants. A larger surface area facilitates the creation of an expansive active surface, thereby significantly enhancing the efficiency of decomposition or oxidation processes. In the context of our study, we have conducted an in-depth investigation into and visually depicted fundamental optical properties, including reflectivity, absorption, refractive index, dielectric function, optical conductivity, and loss functions, for all three crystalline materials, namely Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2, as prominently illustrated in Figs. 4-9.

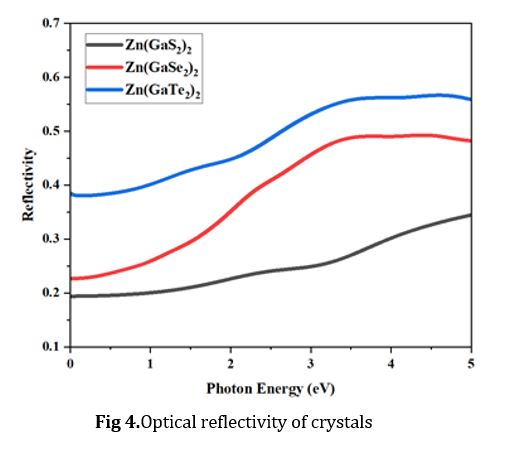
 Optical reflectivity

Optical reflectivity data offers valuable insights into the extent of incident light interacting with the material's surface. Moreover, absorbance is intimately linked to the amount of incident light penetrating the surface. Lower reflectivity corresponds to an increased absorption of the UV or visible light [40]. In this comprehensive investigation, we have meticulously recorded and analyzed the reflectivity patterns exhibited by Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 across an energy spectrum ranging from 0.0 electron volts (eV) to 5.0 eV, as vividly depicted in Fig. 4. Remarkably, these materials consistently display a specific behavior regarding reflectivity within this energy range. Generally, reflectivity exhibits an upward trend with increasing photon energy for all three crystals, showcasing a noteworthy deviation within the photon energy range of 3.0 to 3.5 eV. In the photon energy range spanning from 0.0 to 3.5 eV, Zn (GaTe2)2 emerges as the crystal with the highest reflectivity, followed by Zn(GaSe2)2, while Zn(GaS2)2 exhibits the lowest reflectivity.  These findings underscore the exceptional efficacy of Zn (GaTe2)2 as a highly promising photocatalyst, particularly within the context of its reflectivity characteristics.

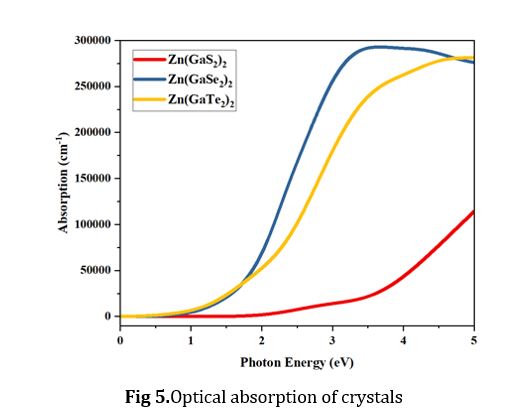
Optical Absorption

The light absorption characteristics of photocatalysts, including crucial attributes such as band gap energy and absorption coefficient, hold paramount significance in comprehending their ability to capture light. It is imperative to emphasize that superior absorption properties indicate enhanced photocatalytic activity. The optical absorption spectra, meticulously recorded for Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2, have been thoughtfully presented in Fig 5. The observed peaks in absorbance correspond to photon transition energies from the maximum valence band (MVB) to the minimum conduction band (MCB) when subjected to the UV and visible light irradiation. This underscores the materials' capability to absorb photons spanning the UV and visible light spectra. Figure 5 elucidates a discernible trend wherein absorbance escalates proportionally with the augmentation of photon energy. Within the photon energy range spanning from 0.0 to 2.0 electron volts (eV), the absorbance exhibited by Zn (GaSe2)2 and Zn (GaTe2)2 is remarkably similar. In contrast, Zn (GaS2)2 deviates significantly, displaying substantially lower absorption when compared to the other two materials in this particular energy range. These findings underscore the distinct absorption characteristics of these materials and their relevance to their photocatalytic potential.

 

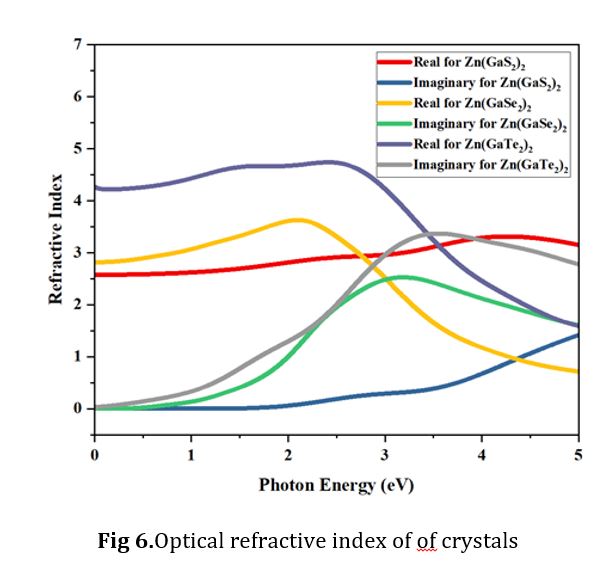
Optical Refractive Index       

The refractive index of a material constitutes a vital parameter in quantifying the absorption of photons during the chemical decomposition process in a solution. It is universally acknowledged that a higher refractive index indicates a more densely packed medium. This relationship can be succinctly elucidated through the definition of a complex refractive index:

 (ω) = η(ω) + iκ(ω)                                    (1)

The fundamental component, denoted as η(ω), of the refractive index characterizes the phase velocity, whereas the imaginary part, κ(ω), is linked to the extinction or absorption coefficient. However, it is worth noting that κ(ω) can also be associated with the mass attenuation coefficient shown in Equation (1), signifying the extent of attenuation experienced by an electromagnetic wave as it traverses the material. As elucidated in a previous study [41], a greater density of the medium is directly correlated with a higher value of the refractive index. Fig. 6 comprehensively depicts the refractive index as a function of photon energy. In this representation, the red, yellow, and light blue lines correspond to the fundamental part of Zn (GaS2)2, Zn (GaSe2)2, and Zn(GaTe2)2, respectively.

 In contrast, the dark cyan, green, and gray lines represent the imaginary part. It is noteworthy that the real part and the imaginary part exhibit an inverse relationship. Initially, the refractive index is higher for the real part at lower photon energies, while the imaginary part remains close to zero. Subsequently, within the photon energy range spanning from 0.0 to 2.0 electron volts (eV), Zn(GaTe2)2 stands out with a higher refractive index for the real and imaginary components, distinguishing it from the other materials in this specific energy range.

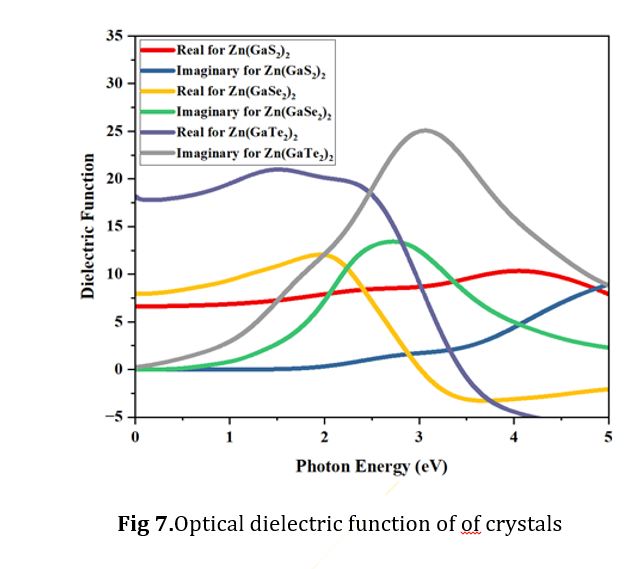
 Dielectric function

The dielectric function is pivotal in the computation of specific optical properties, including reflectivity and refractive index, especially in the context of adsorption on solid materials [42]. To derive ε1(ω) through the Kramers-Kronig relationship involves integrating over a relatively wide frequency range while utilizing the derivative of ε2(ω) as follows:

ε = ε1 (ω) + iε2 (ω)                                    (2)

Where, ε1(ω) signifies the actual component of the dielectric constant, whereas ε2(ω) represents the dielectric loss factor, which constitutes the imaginary part given in Equation (2). Dielectric functions are intrinsic properties of a material that relate to its spatial attributes and are akin to absolute or permittivity. The real part of the dielectric constant plays a role in the storage of potential energy within the electric field, whereas the imaginary amount signifies the converse effect.  Fig. 7 visually presents a consistent trend where the real part of the dielectric function consistently exceeds the imaginary part. In the initial range of photon energy, Zn (GaTe2)2 stands out with the highest values of the dielectric function within the energy span of 0.0 to 2.0 ev.

 

 Optical Conductivity

Electronic transitions hinge on optical conductivity, a parameter intricately connected to the position of electrons between the conduction band and valence band. This relationship takes into account induced current density and electric field effects. It is important to note that these conducting electrons are generated due to the presence of free holes and free electrons within the crystalline material. The relationship between the conductivity for the real part (σ_r) and the imaginary part (σ_i) of the dielectric function ε(ω) is expressed by the following equations: σ_r = ωε_1(ω) and σ_i = ωε_2(ω). As per the equation σ_i =ωε_2(ω), conductivity is directly proportional to both the real and imaginary parts of the dielectric constant. It is essential to highlight that the band gap of an active photocatalyst, situated between the valence band and the conduction band, must be less than 1.8 electron volts (eV) [1]. According to Fig 8, it becomes evident that the difference in conductivity within the photon energy range of 0.0 to 2.0 eV between Zn(GaSe2)2 and Zn(GaTe2)2 is relatively modest.

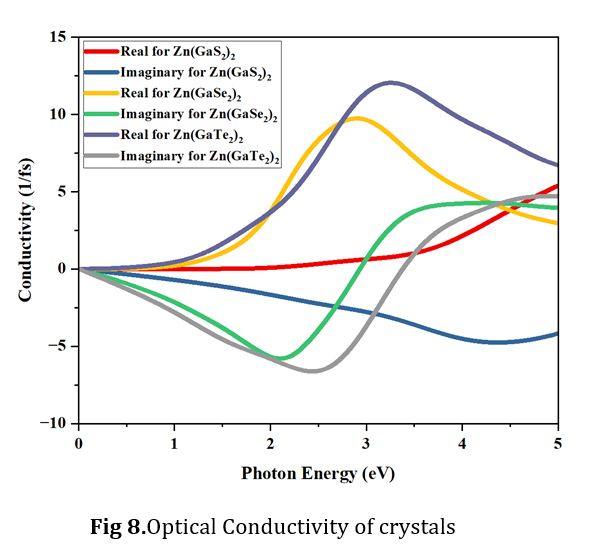
However, with the increase in photon energy, the conductivity of Zn(GaTe2)2 exhibits a notable increase.  It describes how much energy is lost when a fast electron passes through a material. These optical losses are primarily categorized as surface and volume loss functions. The surface energy loss function (SELF) and the volume energy loss function (VELF) delineate the likelihood of photons losing their energy as they propagate through photoactive compounds.

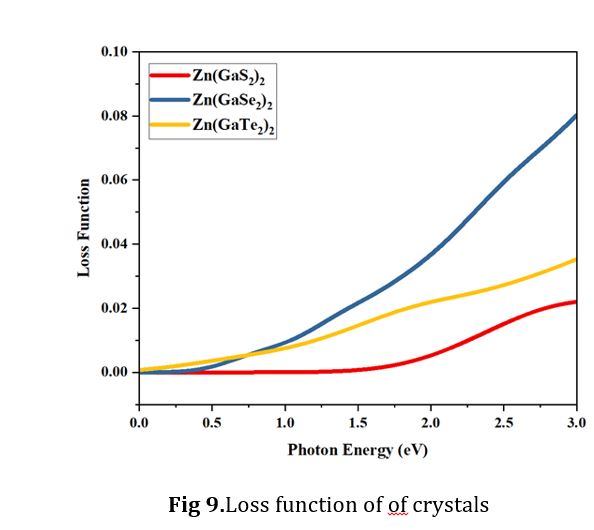
The loss function can be partitioned into two distinct regions based on electronic photon energy: the high photon energy segment and the low photon energy segment. Both of these segments are pivotal for comprehending the optical properties. Notably, the ionization edge, representing the oxidation state of the d orbital splitting for the central atom in complex compounds, fall within the energy range of 2.6 electronvolts (eV) or higher, as depicted in Fig. 9. Specifically, the crystal Zn(GaSe2)2 demonstrates the maximum loss function within the photon energy range of 1.0 to 3.0 eV, signifying the highest d orbital splitting in this particular region. In close succession, Zn (GaTe2)2 in its tetragonal form exhibits the second-highest peak within the same photon energy range.

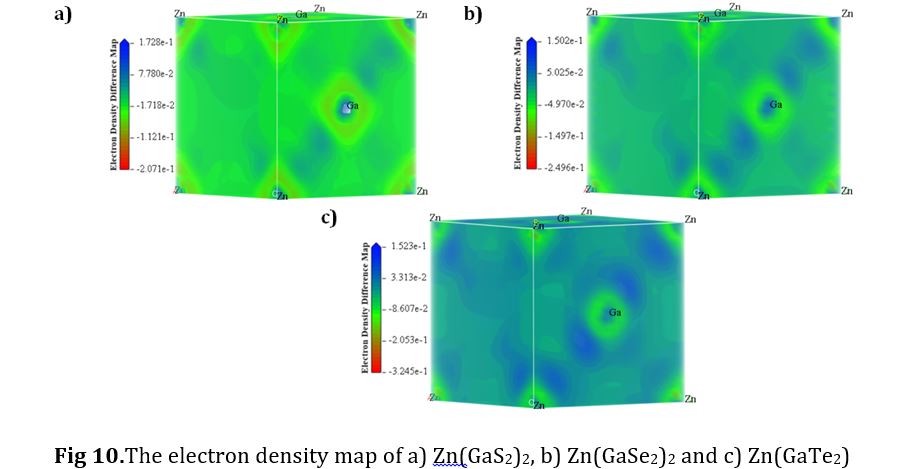
Electron Density Map

The electron density map provides a comprehensive representation of the contents of unit cells, averaging across the entire crystal rather than focusing solely on the contents of a single unit cell. This differentiation becomes particularly critical in situations involving structural disorder. In Fig. 10, the blue marker draws attention to the presence of lone pairs of electrons within the crystals, which have the potential to transition readily from the valence band to the conduction band. However, it's essential to emphasize that the quantification of these lone pairs can be ascertained by examining the electron density map encompassing the entire crystal. In the case of Zn(GaTe2)2, the heightened density of the blue color indicates a larger quantity of lone electron pairs. With an increased abundance of lone electron pairs, the material exhibits a more significant potential for movement between the valence band (VB) and conduction band (CB), thereby suggesting its suitability as a more capable photocatalytic material.

Conclusion

In a comprehensive exploration, this study harnessed first-principle methodologies to scrutinize with utmost precision the intricate facets of electronic structure, structural geometry, quantum properties, and optical attributes inherent to Zn(GaS2)2, Zn(GaSe2)2, and Zn(GaTe2)2 solid crystals. Employing a sophisticated arsenal of four Density Functional Theory (DFT) functionals encompassing the Generalized Gradient Approximation (GGA) approach-specifically, GGA with PBE, GGA with RPBE, GGA with PW91, and GGA with WC-the overarching objective was to elucidate their multifaceted potential as catalysts for photocatalytic processes.

 

Within this vast gamut of GGA functionals enlisted for the intricate task of elucidating electronic structures, GGA with WC emerged as the beacon of accuracy, closely mirroring the empirical values for Zn(GaS2)2. However, the overarching observation unveiled the formidable band gap of Zn (GaS2)2, a towering edifice at 1.936 eV, rendering it an inauspicious candidate for applications in photocatalysis. This yawning chasm in the band structure vastly overshoots the optimal band gap threshold of 1.8 eV, requisite for superior photocatalytic efficacy. Contrastingly, the beguiling Zn(GaSe2)2, with its svelte band gap of 1.726 eV, gracefully positions itself as a compelling option for photocatalytic endeavors, its band energy impeccably nestled within the realm of desirable limits. The pièce de résistance, however, manifested in the form of Zn(GaTe2)2, boasting an astonishingly meager band gap of a mere 0.329 eV, thus anointing it as a veritable powerhouse, singularly efficacious for the purification of wastewater. Furthermore, the three crystals flaunted direct band gaps, an auspicious attribute that expedites the rapid generation of photo-excited electron-hole pairs, an imperative facet of photocatalysis. Among these, Zn(GaSe2)2 shone the brightest, boasting a diminutive band gap that facilitates the effective absorption and utilization of longer-wavelength light-a hallmark of heightened photocatalytic proficiency. Its distinctive band structure, elucidating p-type conductivity attributes, delineates an unhindered flow of electric current within the crystal matrix, endowing it with an innate propensity to engender available holes during redox reactions-a quintessential asset in the crusade against organic pollutants. To sum up, Zn (GaSe2)2 emerges as an enticing convergence of virtues, standing as a beacon of promise for advanced photocatalytic pursuits. Delving deeper into the realm of loss function properties, it becomes patently evident that Zn(GaTe2)2 dons the cloak of diminished loss, signifying a marked reduction in systemic energy dissipation. This alchemical process begets enhanced light emission, rendering it an enchanting candidate for domains immersed in light emission and photonics. Moreover, this same crystalline entity reveals an elevated perch in the dielectric function within the photon energy spectrum of 0.0 to 2.0 eV, signaling considerable potential for integration into the intricate tapestry of optoelectronic devices. These auspicious proclivities beckon forth a chorus of further exploration, for within the annals of this sphere, the tetragonal Zn(GaSe2)2 assumes the mantle of a luminous star, boasting a significantly elevated absorption coefficient-a telltale sign of its adeptness in harnessing and channeling the deluge of incident light. This distinct attribute emboldens its stature as a front-runner among photocatalysts, poised to illuminate the domains of photocatalysis and solar energy conversion.

ORCID

Md Komol Hassan

https://orcid.org/0009-0003-2150-0530

Md Tauhidul Karim

https://orcid.org/0009-0002-7302-5420

Prosenjeet Biswas

https://orcid.org/0009-0006-0610-0549

Debashis Howlader

https://orcid.org/0000-0003-4149-971X

Mohammad Harun-Ur-Rashid:

https://orcid.org/0000-0003-1883-4620

Ajoy Kumer

https://orcid.org/0000-0001-5136-6166

References
  1. Wells MJ, Rossano AJ, Roberts EC. Textile wastewater effluent toxicity identification evaluation. Archives of Environmental Contamination and Toxicology. 1994 Nov;27:555-60. [Crossref], [Google Scholar], [Publisher]
  2. Olukanni OD, Osuntoki AA, Gbenle GO. Textile effluent biodegradation potentials of textile effluent-adapted and non-adapted bacteria. African Journal of Biotechnology. 2006;5(20). [Google Scholar], [Publisher]
  3. Hossain L, Sarker SK, Khan MS. Evaluation of present and future wastewater impacts of textile dyeing industries in Bangladesh. Environmental Development. 2018 Jun 1;26:23-33. [Crossref], [Google Scholar], [Publisher]
  4. Moniz SJ, Shevlin SA, Martin DJ, Guo ZX, Tang J. Visible-light driven heterojunction photocatalysts for water splitting–a critical review. Energy & Environmental Science. 2015;8(3):731-59. [Crossref], [Google Scholar], [Publisher]
  5. Ni M, Leung MK, Leung DY, Sumathy K. A review and recent developments in photocatalytic water-splitting using TiO2 for hydrogen production. Renewable and Sustainable Energy Reviews. 2007 Apr 1;11(3):401-25. [Crossref], [Google Scholar], [Publisher]
  6. Xia T, Lin Y, Li W, Ju M. Photocatalytic degradation of organic pollutants by MOFs based materials: A review. Chinese Chemical Letters. 2021 Oct 1;32(10):2975-84. [Crossref], [Google Scholar], [Publisher]
  7. Chen S, Hu Y, Meng S, Fu X. Study on the separation mechanisms of photogenerated electrons and holes for composite photocatalysts g-C3N4-WO3. Applied Catalysis B: Environmental. 2014 May 5;150:564-73. [Crossref], [Google Scholar], [Publisher]
  8. Yu Y, Cao C, Liu H, Li P, Wei F, Jiang Y, Song W. A Bi/BiOCl heterojunction photocatalyst with enhanced electron–hole separation and excellent visible light photodegrading activity. Journal of Materials Chemistry A. 2014;2(6):1677-81. [Crossref], [Google Scholar], [Publisher]
  9. Lee SS, Bai H, Liu Z, Sun DD. Green approach for photocatalytic Cu (II)-EDTA degradation over TiO2: toward environmental sustainability. Environmental science & technology. 2015 Feb 17;49(4):2541-8. [Crossref], [Google Scholar], [Publisher]
  10. Islam MJ, Kumer A. First-principles study of structural, electronic and optical properties of AgSbO3 and AgSb0. 78Se0. 22O3 photocatalyst. SN Applied Sciences. 2020 Feb;2(2):251. [Crossref], [Google Scholar], [Publisher]
  11. Li G, Hou J, Zhang W, Li P, Liu G, Wang Y, Wang K. Graphene-bridged WO3/MoS2 Z-scheme photocatalyst for enhanced photodegradation under visible light irradiation. Materials Chemistry and Physics. 2020 May 1;246:122827. [Crossref], [Google Scholar], [Publisher]
  12. Li G, Nie X, Chen J, Jiang Q, An T, Wong PK, Zhang H, Zhao H, Yamashita H. Enhanced visible-light-driven photocatalytic inactivation of Escherichia coli using g-C3N4/TiO2 hybrid photocatalyst synthesized using a hydrothermal-calcination approach. Water research. 2015 Dec 1;86:17-24. [Crossref], [Google Scholar], [Publisher]
  13. Hasan MM, Kumer A, Chakma U, Islam MT. Structural, optical and electronic properties of ZnAg2GeTe4 and ZnAg2Ge0. 93Fe0. 07Te4 photocatalyst: a first principle approach. Molecular Simulation. 2021 May 3;47(7):594-601. [Crossref], [Google Scholar], [Publisher]
  14. Shi H, Chen J, Li G, Nie X, Zhao H, Wong PK, An T. Synthesis and characterization of novel plasmonic Ag/AgX-CNTs (X= Cl, Br, I) nanocomposite photocatalysts and synergetic degradation of organic pollutant under visible light. ACS applied materials & interfaces. 2013 Aug 14;5(15):6959-67. [Crossref], [Google Scholar], [Publisher]
  15. Xing J, Jiang HB, Chen JF, Li YH, Wu L, Yang S, Zheng LR, Wang HF, Hu P, Zhao HJ, Yang HG. Active sites on hydrogen evolution photocatalyst. Journal of Materials Chemistry A. 2013;1(48):15258-64. [Crossref], [Google Scholar], [Publisher]
  16. Liu J. Origin of high photocatalytic efficiency in monolayer g-C3N4/CdS heterostructure: a hybrid DFT study. The Journal of Physical Chemistry C. 2015 Dec 24;119(51):28417-23. [Crossref], [Google Scholar], [Publisher]
  17. Cheng P, Wang Y, Xu L, Sun P, Su Z, Jin F, Liu F, Sun Y, Lu G. High specific surface area urchin-like hierarchical ZnO-TiO2 architectures: hydrothermal synthesis and photocatalytic properties. Materials Letters. 2016 Jul 15;175:52-5. [Crossref], [Google Scholar], [Publisher]
  18. Pereira JH, Vilar VJ, Borges MT, González O, Esplugas S, Boaventura RA. Photocatalytic degradation of oxytetracycline using TiO2 under natural and simulated solar radiation. solar energy. 2011 Nov 1;85(11):2732-40. [Crossref], [Google Scholar], [Publisher]
  19. Xu J, Zhang L, Shi R, Zhu Y. Chemical exfoliation of graphitic carbon nitride for efficient heterogeneous photocatalysis. Journal of Materials Chemistry A. 2013;1(46):14766-72. [Crossref], [Google Scholar], [Publisher]
  20. Herrmann JM. Heterogeneous photocatalysis: fundamentals and applications to the removal of various types of aqueous pollutants. Catalysis today. 1999 Oct 15;53(1):115-29. [Crossref], [Google Scholar], [Publisher]
  21. Chen X, Wu Z, Liu D, Gao Z. Preparation of ZnO photocatalyst for the efficient and rapid photocatalytic degradation of azo dyes. Nanoscale research letters. 2017 Dec;12:1-0. [Crossref], [Google Scholar], [Publisher]
  22. Yıldırım ÖA, Unalan HE, Durucan C. Highly efficient room temperature synthesis of silver‐doped zinc oxide (ZnO: Ag) nanoparticles: structural, optical, and photocatalytic properties. Journal of the American Ceramic Society. 2013 Mar;96(3):766-73. [Crossref], [Google Scholar], [Publisher]
  23. Mohamed MA, Salleh WN, Jaafar J, Rosmi MS, Hir ZA, Abd Mutalib M, Ismail AF, Tanemura M. Carbon as amorphous shell and interstitial dopant in mesoporous rutile TiO2: Bio-template assisted sol-gel synthesis and photocatalytic activity. Applied Surface Science. 2017 Jan 30;393:46-59. [Crossref], [Google Scholar], [Publisher]
  24. Rengifo-Herrera JA, Pulgarin C. Photocatalytic activity of N, S co-doped and N-doped commercial anatase TiO2 powders towards phenol oxidation and E. coli inactivation under simulated solar light irradiation. Solar Energy. 2010 Jan 1;84(1):37-43. [Crossref], [Google Scholar], [Publisher]
  25. Yu S, Yun HJ, Kim YH, Yi J. Carbon-doped TiO2 nanoparticles wrapped with nanographene as a high performance photocatalyst for phenol degradation under visible light irradiation. Applied Catalysis B: Environmental. 2014 Jan 1;144:893-9. [Crossref], [Google Scholar], [Publisher]
  26. Mohamed MA, Salleh WN, Jaafar J, Ismail AF, Abd Mutalib M, Jamil SM. Incorporation of N-doped TiO2 nanorods in regenerated cellulose thin films fabricated from recycled newspaper as a green portable photocatalyst. Carbohydrate polymers. 2015 Nov 20;133:429-37. [Crossref], [Google Scholar], [Publisher]
  27. Zhang Z, Shao C, Li X, Zhang L, Xue H, Wang C, Liu Y. Electrospun nanofibers of ZnO− SnO2 heterojunction with high photocatalytic activity. The Journal of Physical Chemistry C. 2010 May 6;114(17):7920-5. [Crossref], [Google Scholar], [Publisher]
  28. Lin L, Yang Y, Men L, Wang X, He D, Chai Y, Zhao B, Ghoshroy S, Tang Q. A highly efficient TiO 2@ ZnO n–p–n heterojunction nanorod photocatalyst. Nanoscale. 2013;5(2):588-93. [Crossref], [Google Scholar], [Publisher]
  29. Chong MN, Jin B, Chow CW, Saint C. Recent developments in photocatalytic water treatment technology: a review. Water research. 2010 May 1;44(10):2997-3027. [Crossref], [Google Scholar], [Publisher]
  30. Cheng P, Wang Y, Xu L, Sun P, Su Z, Jin F, Liu F, Sun Y, Lu G. High specific surface area urchin-like hierarchical ZnO-TiO2 architectures: hydrothermal synthesis and photocatalytic properties. Materials Letters. 2016 Jul 15;175:52-5. [Crossref], [Google Scholar], [Publisher]
  31. Ledoux MJ, Pham-Huu C. High specific surface area carbides of silicon and transition metals for catalysis. Catalysis today. 1992 Jun 30;15(2):263-84. [Crossref], [Google Scholar], [Publisher]
  32. Russell AS, Stokes Jr JJ. Role of surface area in dehydrocyclization catalysis. Industrial & Engineering Chemistry. 1946 Oct;38(10):1071-4. [Crossref], [Google Scholar], [Publisher]
  33. Ren Y, Hu Y, Hu Z, Xue L. First-principles study on electronic and optical properties of Zn-substituted CuGaSe2. Results in Physics. 2021 Jan 1;20:103774. [Crossref], [Google Scholar], [Publisher]
  34. Chen C, Lin Z, Wang ZS. The development of new borate-based UV nonlinear optical crystals. Applied Physics B. 2005 Jan;80:1-25. [Crossref], [Google Scholar], [Publisher]
  35. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Physical review letters. 1996 Oct 28;77(18):3865. [Crossref], [Google Scholar], [Publisher]
  36. Parr RG, Szentpály LV, Liu S. Electrophilicity index. Journal of the American Chemical Society. 1999 Mar 10;121(9):1922-4. [Crossref], [Google Scholar], [Publisher]
  37. Parr RG, Chattaraj PK. Principle of maximum hardness. Journal of the American Chemical Society. 1991 Feb;113(5):1854-5. [Crossref], [Google Scholar], [Publisher]
  38. Ziesche P, Kurth S, Perdew JP. Density functionals from LDA to GGA. Computational materials science. 1998 Apr 1;11(2):122-7. [Crossref], [Google Scholar], [Publisher]
  39. Kurth S, Perdew JP, Blaha P. Molecular and solid‐state tests of density functional approximations: LSD, GGAs, and meta‐GGAs. International journal of quantum chemistry. 1999;75(4‐5):889-909. [Crossref], [Google Scholar], [Publisher]
  40. Berning PH, Hass G, Madden RP. Reflectance-increasing coatings for the vacuum ultraviolet and their applications. JOSA. 1960 Jun 1;50(6):586-97. [Crossref], [Google Scholar], [Publisher]
  41. Simmons Jr FL, Ferrante R, inventors; Simtek Hardcoatings Inc, assignee. UV reflective photocatalytic dielectric combiner having indices of refraction greater than 2.0. United States patent US 6,154,311. 2000 Nov 28. [Google Scholar], [Publisher]
  42. Bertsch GF, Iwata JI, Rubio A, Yabana K. Real-space, real-time method for the dielectric function. Physical Review B. 2000 Sep 15;62(12):7998. [Crossref], [Google Scholar], [Publisher]

     

    Citation: ­­­­­ Md. Komol Hassan, Md Tauhidul Karim, Prosenjeet Biswas, Debashis Howlader, Md Harun Ur Rashid, Ajoy Kumer. Computational Investigation for Tetragonal Crystals of Zn (GaS2)2, Zn (GaSe2)2, and Zn (GaTe2)2 Photocatalysts for Wastewater Treatment: First Principle Approaches, Ad. J. Chem. B, 6 (2024) 46-66

    https://doi.org/10.48309/ajcb.2024.421434.1204  
Advanced Journal of Chemistry, Section B: Natural Products and Medical Chemistry
Volume 6, Issue 1 - Serial Number 1
February 2024
Pages 46-66
Files
History
  • Receive Date: 19 October 2023
  • Revise Date: 08 November 2023
  • Accept Date: 20 December 2023
Share
How to cite
Statistics